Fall 2011 to Spring 2012
Fall 2012 to Spring 2013
Fall 2013 to Spring 2014
Fall 2014 to Spring 2015
Cambridge, King Open School, Grade 4
In these two trials, we spent five weeks in two 4th grade classrooms, one with 21 students, one with 19. For each class, we ported onto tablets an entire unit of math curriculum from TERC’s Investigations curriculum. This porting process was instructive, as we had to deal with the fact that the tablet screen is smaller than the printed page. As a result, the electronic notebook for a 40-page paper unit was over 100 pages long and students sometimes had to work on 10 to 12 separate electronic pages in one class period, rather than the 2-3 paper pages they would normally be assigned. Psychologically, this was an issue for some students, especially those who had organizational challenges, and teachers came up with a variety of record-keeping strategies to help students not feel overwhelmed by the number of pages. We are quite concerned about these and other often-unacknowledged issues of “digitizing” paper curricula, especially as devices get progressively smaller, and plan to write a position paper about them in the next year.
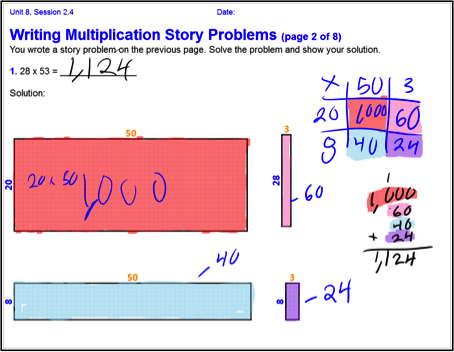
In these two field tests, students in both classrooms were studying multiplication and division. In the Fall the emphasis was more on multiplication and, in particular, on how to simplify a 2-digit by 2-digit multiplication problem by dividing it into partial products or relating it to a simpler problem. In the Spring there was more emphasis on division. In both classes, students used array creation and manipulation tools extensively; these were especially useful to help students visualize the relationship between partial products and the original problem. In one class, the teacher encouraged students to be explicit about this correspondence using colors to highlight the areas of an array represented by each partial product. Figure 1 illustrates one student’s work using the highlighter tool to color-code corresponding areas and equations. To illustrate her solution to 28 x 53, the student created a 28x53 array using CLP’s array tool, then cut it into four smaller arrays using the “cut” tool. These arrays corresponded to the partial products formed by dividing each factor by place value: 20 x 50, 20 x 3, 50 x 8 and 8 x 3. This student had learned the “box” method, shown in the upper right of her work, which is a graphical device for separating factors by place value, but until she saw the correspondence with the array model, her use of the box was rote, and she didn’t understand why it “worked.”
Figure 1: Student work showing the correspondence between computed partial products and the areas they represent by color-coding. The student created a 28x53 array, then cut it into four arrays that represent the four partial products using a “cut” tool provided by CLP.
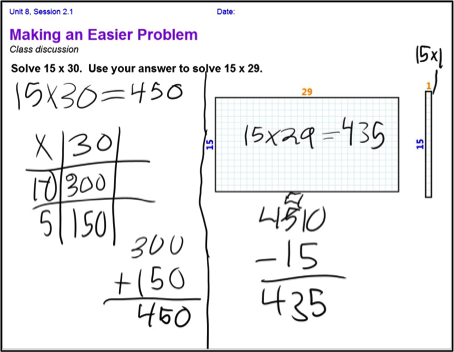
In Figure 2 is another example of the way in which our array creation and manipulation tools helped students gain a deeper understanding of multiplication. The curriculum contains several problems in which students are instructed to solve a multiplication problem such as 15 x 29 by considering how it relates to a simpler problem such as 15 x 30. Students often have a problem figuring out how to modify their answer to 15 x 30 to get 15 x 29; a common error students make is to subtract 1 from their answer to 15 x 30, rather than subtracting 15. Visualizing “subtracting 1 from 30” as cutting off a row of an array made it clearer to this student that the difference between a 15x30 array and a 15x29 array is a row of 15. After working with the array tool on problems like this, she consistently referred to “groups of N” in her work with related multiplication problems.
Figure 2: Student work illustrating the process of solving 15 x 29 using the easier problem 15 x 30
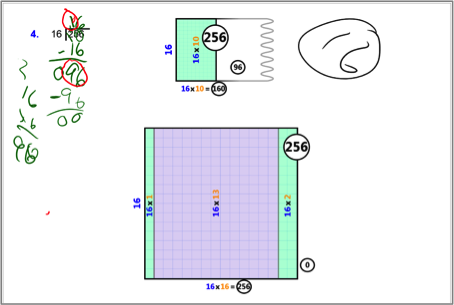
In the Spring trial, we introduced the division tool, which proved very popular with students; in an end-of-unit survey, most students in the class identified the division tool as their favorite aspect of the system. We are in the process of analyzing students’ work with the division tool to gauge its impact on their reasoning about division and, in particular, about remainders. One particular compelling example of the utility of the tool appeared in an interview we conducted with one of the high-achieving math students at the end of our intervention. This student was quite fluent in his ability to do long division using the traditional algorithm. Below in Figure 3, we can see his solution to 256 ÷ 16 by the traditional method. Then we asked him to do the problem using the division tool. In parallel, with the way he had already solved the problem, he began with a 16x1 array, mimicking his “1” as the first digit of the solution. When he saw what happened, he was puzzled, because, as he said, “I thought this (referring to his long division problem) would be the same as the division tool….but it’s not.” The interviewer proceeded to show the student what would happen if he had added a 16x10 array rather than a 16x1 array. For this student, this was a major breakthrough, as he said, “I never thought of this (circling the 1 in his long division solution with red ink). I just thought of this as a 1, but it’s really a 10.”
Figure 3: Work generated as part of an interview in which a student understood something new about the long division algorithm
Our analysis and writing in the upcoming year will focus on evidence of the affordances and effects of these digital tools on students’ mathematical reasoning, especially about multiplicative structures.