Fall 2011 to Spring 2012
Fall 2012 to Spring 2013
Fall 2013 to Spring 2014
Fall 2014 to Spring 2015
Cambridge, Maria L. Baldwin School, Grade 4
Our field test with 4th graders at the Baldwin School was designed to investigate the impact of the array tool on students’ understanding of multiplication, especially problems involving 2-digit by 2-digit multiplication in which working with partial products was a useful strategy. We hypothesized that the array tool would allow students to visualize the relationships between the original problem (e.g., 37 x 46) and the partial products that might contribute to solving the original problem (e.g., 30 x 40, 30 x 6 or 7 x 6).
Without a visual representation of a multiplication problem, students have a tendency to lose track of some of the partial products; a common student error is to say, e.g., that 46 x 37 = 40 x 30 + 6 x 7. In using the “standard algorithm,” students often get confused about place value and misalign their partial products. The curriculum being used in our field test classroom—Investigations in Number, Data, and Space—emphasizes the use of arrays as a way of understanding the mechanics of multi-digit multiplication, so it was a natural place to try out the array tool.
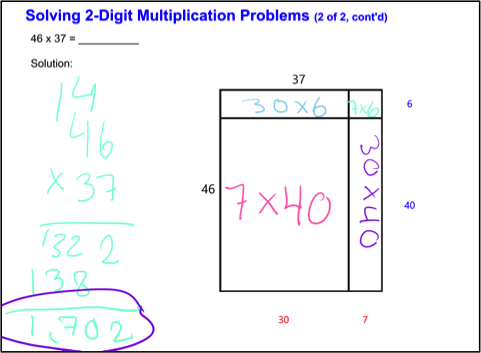
One of the issues that both teachers and math educators have noticed is that some students are not clear about the correspondence between the numbers on the sides of an array and the area inside the array. We noticed this happening with some students in our field test. Students who lacked clarity about the process and goal of dividing up the array had trouble associating the numbers that labeled the “splits” with the corresponding area inside the array. This was probably exacerbated by the fact that in our array tool, the numbers corresponding to the original multiplication problem and the original array were located on the left and above the array, while the numbers corresponding to the partitions of each side were on the bottom and right. See Figure 1 for an example of how the sides and partitions of the array were labeled. In our next version, labels for the splits will be next to the labels for the original lengths of the sides.
Figure 1: Using the array tool.
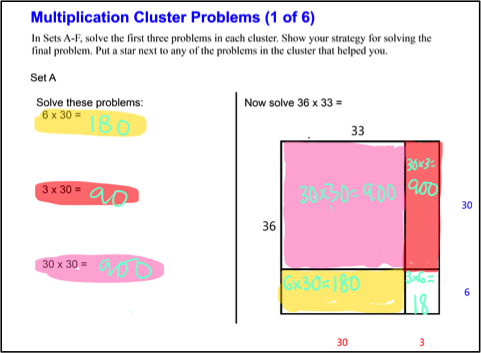
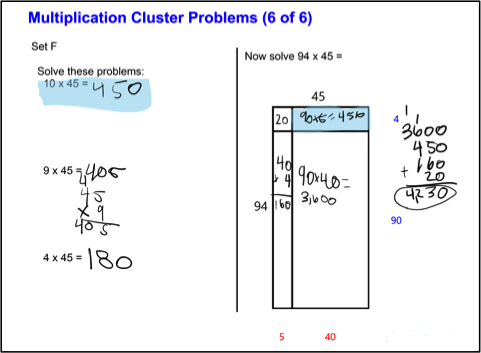
Many of the problems students worked with the array tool were “cluster problems,” in which they were to work three preliminary problems, then use one or more of them to help solve a more complex problem. Figure 2 illustrates this kind of problem, done using the array tool. The teacher reinforced the correspondence between the partial products and their representation in the array by asking students to color-code the subparts of the array and their corresponding cluster problems.
Figure 2: Solving a cluster problem and shading corresponding partial products
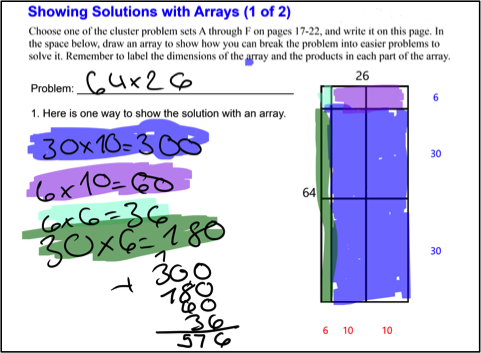
Our array tool supports any number of divisions along either side of the array, and some students took advantage of this capability. Figure 3 shows the work of one student who was quite facile figuring out simpler problems and visualizing them on the array, though she mislabeled one of the splits. Some students even used the divider capability to explore some unusual equivalences, as in Figure 4. This student discovered that 33 x 36 could also be represented as 12 boxes of 99, then used the standard algorithm to do the (easier) problem 99 x 12.
Figure 3: Using multiple dividers on each side of an array to solve a multiplication problem; the software could give feedback to the student about the mistake in split for 64
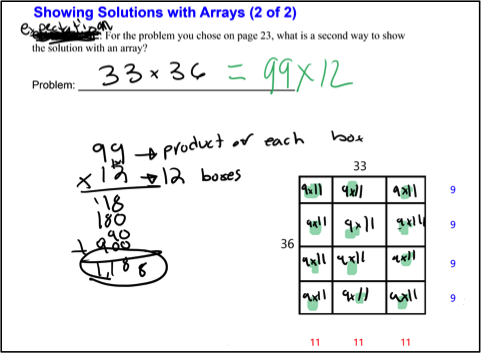
This explanation and picture helped many of the students, and the next day, a significant portion of the student work reflected the array structure, as shown in Figure 4.
Figure 4: Discovering a multiplicative equivalence
The current version of the array tool does not provide any feedback to the student, but that capability could be added and we will be exploring that possibility next year. In Figure 3, for example, the student entered a 6 instead of a 4 for one of the splits for 63. The software could identify this mistake and let the student know. More difficult for the software to identify is the mistake shown in Figure 5. In this example, the student has labeled the splits of each dimension accurately, but has mislabeled the areas inside the array. The area labeled 90 x 5 is actually 40 x 4 and vice-versa. The software would have to employ handwriting recognition techniques or provide an alternative to handwritten partial product information in order to identify this mistake.
Figure 5: A place where handwriting recognition or alternative to handwritten partial product information would be needed in order for software to provide feedback to student
While we were not specifically studying how our system affected interactions between the teacher and students, we observed an interesting affordance of the communication aspect of the tablets in this class. As she usually did, the teacher gathered a small group of students who self-identified as having difficulty with the math problems around her on the floor to work as a small group. What was unusual, however, was that she was pregnant at the time and was unable to do what she usually did: get up from the floor to walk around and check the work her other students were doing. In this setting, our system made it possible for her to check and comment on other students’ work without leaving the group on the floor. As students submitted their work, she would quickly look it over on her tablet, then, if necessary, give them individual feedback, such as, “John, please check your answer on page 4,” or “Mary, you didn’t highlight the part of the array that corresponded to the problem you circled,” or, if she noticed a common issue, “I see that many people are just dividing numbers into tens and ones. See if you can find a different strategy.”
In classrooms where teachers are often trying to differentiate instruction for several groups of students, systems such as ours can play a particularly useful role in allowing teachers to work intensely with a small group while continuing to monitor and respond to the rest of the class. Our current system allows teachers to see what each student has submitted, page by page, including if students have made several submissions, e.g., a second submission revising a first incorrect one. In this coming year, we will integrate the artificial intelligence analysis and sorting tools that have been developed with the teacher submission viewer so that she can get a quick overview of the strategies students are using and will develop ways for the teacher to send individualized problems to students in response to their work.