Fall 2011 to Spring 2012
Fall 2012 to Spring 2013
Fall 2013 to Spring 2014
Fall 2014 to Spring 2015
Waltham, Northeast Elementary School, Grades 4 & 5 (Special needs)
Instructional Materials: Two trials, each with curriculum materials focusing on multiplication and division
The INK-12 project conducted two classroom trials for a total of 10 sessions of between 45 minutes and an hour in a substantially separate class of students with disabilities at the Northeast School in Waltham, MA. Students are assigned to this class based on having IQs below 70 as determined by district/state tests, but no behavioral issues such as autism. The class included two students who had limited knowledge of English and others who had difficulties with focusing and attention. For the first three sessions the class consisted of eight students. After that, one student moved to another town, so that for the second set of seven sessions, the class had only seven students. The focus of the mathematics was multiplication and division. The teacher had been working with the students on their multiplication facts, but did not have the resources to work on building conceptual understanding of the operations. She welcomed the INK-12 project as a way to help her students develop mathematical understanding beyond memorizing the facts.
The lessons in the first four sessions were built around using stamps to solve multiplication story problems. At first, a pre-made stamp was introduced, with the object in the story already drawn. Mickey's work in Figure 1a has a clear organization for the cookie stamps and uses a reliable strategy of counting by 2's to solve the problem. Other students, such as Eliza, used the stamps and repeated addition to solve the problem, as shown in Figure 1b.
Figure 1a. Mickey's work using stamps for 4 x 6.

Figure 1b. Eliza's work using stamps for 4 x 6.

Subsequently, problems were introduced in which students drew their own object on the stamp. The students were engaged by being able to make their own representations. The teacher reported that in addition to engaging the students, the stamps helped students organize their thinking, and kept them from perseverating over details of the drawing. The students with a limited knowledge of English did particularly well when they were able to draw their own stamps. Hector created a stamp of a car with four wheels, created several copies of it and used repeated addition to solve a multiplication problem about wheels, as shown in Figure 2a. When he had been asked a similar wheel problem orally, he had not been able to solve it. Hector also developed a reliable way to do division problems using a dealing out strategy with his own stamps, as shown in Figure 2b. Although he did not write the number sentence correctly, he represented the problem correctly and knew what all of the parts were.
Figure 2a. Hector's work using a car stamp.

Figure 2b. Hector's work using a pencil stamp.
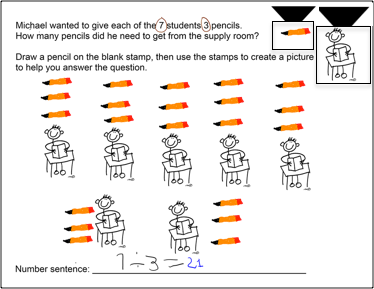
Alfonso, another student with limited English proficiency, had more success drawing his own stamps, as opposed to using the pre-made stamps. He had some fine motor control difficulties with the pre-made stamps, which frustrated him. Figure 3a shows Alfonso's work using pre-made stamps. Although he solved this division problem correctly, the representation did not show 18 cookies, and he had a hard time moving the stamps. When he created his own stamp with 3 stickers on it for the problem: "if each student gets 3 stickers and there are 8 students, how many stickers are there in all?" he was able to represent and solve the problem correctly, as shown in Figure 3b. Alfonso was also able to use his drawings to correctly solve some division problems, as shown in Figure 14c, even though when we started working with the class, Alfonso did not understand what division was and was unable to answer any division questions on the pre-assessment.
Figure 3a. Alfonso's work with a premade stamp.
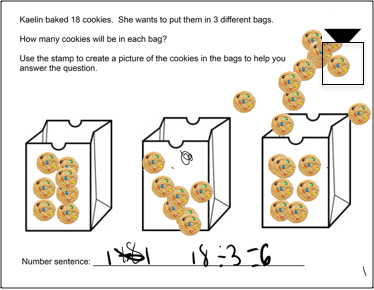
Figure 3b. Alfonso's work with his own drawn stamp.

Figure 3c: Alfonso's division work with his own stamps.

For some students, extended practice using stamps appeared to facilitate significant growth in their thinking. During one lesson using stamps, Mickey went from not representing the correct problem, to being able to represent and solve a problem correctly, to being able to write, represent, and solve his own number problem, as shown in Figure 4 a through d. While this student, as well as the others, still needs a lot of practice to solidify his understanding, this success can be a foundation for future work with multiplication and division.
Figure 4a. Mickey's work: incorrect problem.
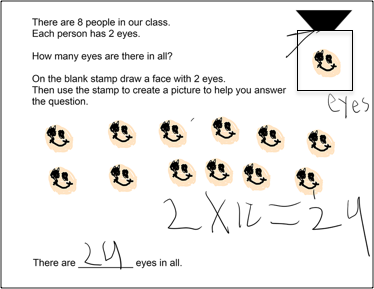
Figure 4b. Mickey's work: correct problem.

Figure 4c. Mickey's work: correct problem.

Figure 4d. Mickey's own problem.

The next four lessons used tiles, virtual manipulatives that could be used individually or combined into stacks, which we called "towers." These lessons involved "The Tower Game," based on a paper by Tzur, R., et al: Students with Learning Disability in Math are Left Behind in Multiplicative Reasoning? Number as Abstract Composite Unit is a Likely 'Culprit.' In The Tower Game, students draw cards that specify how many towers they should build and how many cubes are in each tower, then they use these to compute a total number of cubes. (For an example of the Tower Game, see Figure 5a). In the first lesson, the students played the game using physical snap cubes and building actual towers. They were able to do this, although they had some trouble keeping track of what each number in the number sentence represented and how the number sentence related to the snap cubes. During the next session, they played the game using tiles on the computer rather than physical cubes, as in Figure 5b . They then moved on to story problems with a similar multiplicative structure, writing a number sentence to match the story, and using shapes to indicate "objects" (analogous to "tiles") and "groups" (analogous to "towers"). Words such as "groups" and "objects" provided very difficult for these students, so the constraints of the lesson were changed so that they could use labels that were specific to each problem, as shown in Figure 6.
Figure 5a. The structure of the Tower Game.
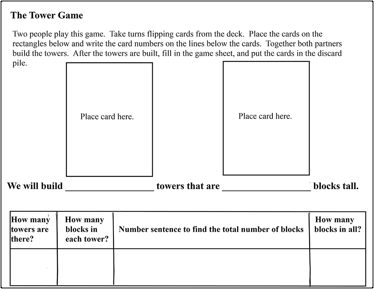
Figure 5b. Using tiles to play the Tower Game.
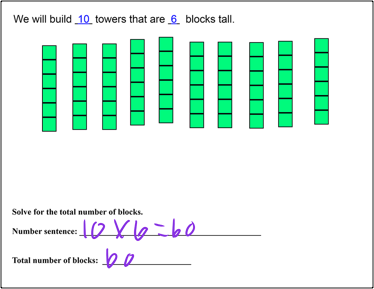
Figure 6: Substituting specific labels for "group" and "object".
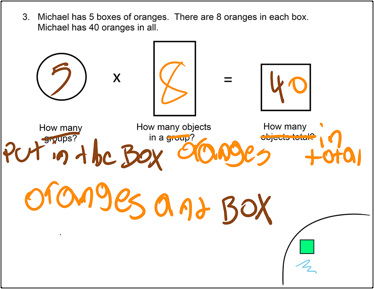
Since the tiles were cumbersome for some students, they were also given their choice of using stamps or freehand drawing to represent a number sentence. Most students chose stamps or drawings, but some students had success with the tiles. The tiles and the structure of the problems appeared to be particularly helpful for Nelson, a student who had issues with focusing. Without the tiles and the problem structure, Nelson would race through a problem by either just writing a number sentence that might have the right answer but didn't match the problem, as in Figure 7a, or by drawing a representation that didn't match the problem at all, as in Figure 7b. With the tiles, he was able to represent and solve the two similar problems in Figures 8a and 8b correctly.
Figure 7a. Nelson's work: incorrect problem.
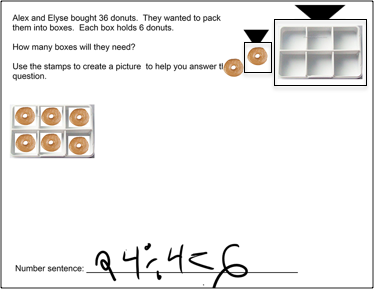
Figure 7b. Nelson's work: incorrect problem.

Figure 8a. Nelson's work with tiles.
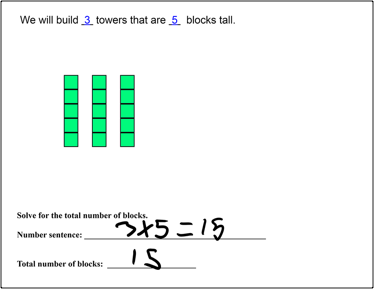
Figure 8b. Nelson's work with tiles.

All students had some success solving multiplication and division with the tiles, however, deciding between multiplication and division was difficult for the students. Division was especially challenging, as the students had relatively limited experience with this operation. Some students solved division problems correctly but their number sentences did not match their representations. Some students had the correct representation, but an incorrect number sentence. Some students could write a multiplication sentence that represented the division situation, but were unsure which number in the sentence was the required answer. Again, these students need repeated practice with predictable structures, such as the stamps or tiles, to solidify their knowledge of these operations.
Pre- and post-assessments with multiplication and division items were administered, both orally and in written form, to all the students in this class. Items included multiplication and division computation, solving story problems, and problems involving visualization, e.g., If there are 3 tennis balls in one can, how many are there in 4 cans?
The assessments suggest that the students from this substantially separate class made some progress in solving multiplication and division problems through their experience using the tablets. On the post-assessment, they were more confident in their ability to solve problems. They all had a strategy for each problem, even if it was counting by 1s and were more likely to explain how they got an answer than they had been on the pre-assessment. For example:
- For 20÷5 one student said that she put cubes in her head, indicating that she put 20 in 5 groups of 4.
- For 4x3, one student said , "I know 3x3 is 9 and then he said 10,11,12."
- ne student solved 10÷2 by going remembering that 5+5 = 10 and reasoning that there were 2 groups of 5 in 10.
- One student said "36÷6 is 6 because 6x6=36."
As there had been during the class sessions, there was considerable variability in students' ability to connect representations with number sentences on the post-assessment. Although a few students were able to connect representations with number sentences on the post-assessment, others were not. For example, for 7x3, some students drew 7 things and 3 things (as opposed to 7 groups of 3), but had the correct number sentence. It was also difficult for them to connect real-life contexts with what they know. For example, they might know 8x2=16, but be unable to answer the question: "If there are 8 stickers on one page, how many are there on 2 pages?"
In summary, data from the field test, the assessments, and the post-field test teacher interview, conducted by the evaluator, indicate that the students in the class gained confidence through their use of the tablet computers. The use of the stamp feature for most of the students, and the tiles for a few of them, helped them organize their thinking and limited their tendency to perseverate and erase, thus facilitating their understanding of multiplication and division. Although the sharing of student work was not as powerful in this class as others, probably because the class does not often engage in discussion and because of the attention difficulties of some, the students were empowered by seeing their name on the large monitor, and their work referred to as an example of a particular strategy or representation.