Fall 2011 to Spring 2012
Fall 2012 to Spring 2013
Fall 2013 to Spring 2014
Fall 2014 to Spring 2015
Waltham, Northeast Elementary School, Grade 4
Instructional Materials:
First trial: MCAS (Massachusetts standardized state test, which students take in May) prep problems, drawn from previous years' MCAS items in one trial
Second trial: Other curriculum materials, focusing on multiplication, division, and proportional reasoning
Working in this class inadvertently allowed us to investigate just how far the technology "novelty" factor would stretch. Not only were we in her class for eight days, but most of the math work students did was relatively unexciting, as it was test preparation. The results were mixed. We definitely saw students' interest decrease to the point that they did not seem excited to see us arrive with the tablets. When we interviewed them about their experiences using the tablets, however, they were still very enthusiastic and insisted that it was more fun to do math using the computers.
An interesting design decision arose in the context of students' work on basic fraction concepts. A simple problem uncovered some serious gaps in students' understanding of fractions, as shown in Figure 1, students'
Figure 1: Student representations of fractions showing a lack of understanding of the idea of a "consistent whole."
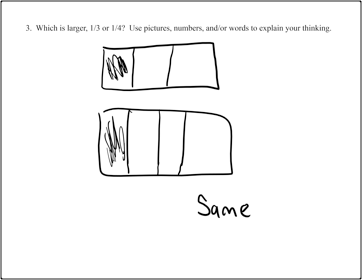

It became clear that some students didn't have a firm grasp on the idea of a "consistent whole," i.e., that in comparing two fractions, it is important that the whole be the same size. They seemed to have less of a problem doing fraction problems where the whole was a set of discrete objects (e.g., Ms. Tyler has 14 flowers. 2/7 of them are red. How many flowers are red?), since the size of the whole was explicitly given. But when it came to fractional problems involving area where students had to 1) draw the whole, and 2) divide it up into equal-area pieces, some students struggled. The student whose work is shown on the left in Figure 1 exhibits both problems: His wholes aren't equal and he hasn't partitioned the wholes into equal parts. The student whose work is on the right in Figure 1 has also drawn unequal wholes that are even different shapes, and it's unclear both how she decided to divide up the shapes and what relationship her picture has to her answer.
In light of these experiences, we discussed the possibility of implementing drawing tools for creating and partitioning representations of area models for fractions. We considered a tool that would draw equal-sized "wholes" for students and tools that would automatically divide a whole into some number of equal parts, as specified by the student. These kinds of tools would keep students from creating the kinds of representations shown above—and drawing incorrect conclusions based on them. On the other hand, students need to actively recognize the importance of having equal-sized wholes, and it's possible that having tools that do this work for them would circumvent their understanding. The jury is still out on this question; we plan to look at the kinds of tools other math educators have developed to support fractional reasoning (e.g., Dynamic Number from Key Curriculum Press) and consider integrating them into the our software.
We also introduced two new features in this class, which are described in the Technology section (Section 3): teachers' ability to replay the way that students solved problems, and students' ability to make audio recordings of explanations.
Ink replay. The students were asked to complete the following math problem: "Henry wants to plant 24 tomato seeds in the school garden. There are 4 rows. How many seeds does he plant in each row? Write a number sentence, and circle the number that answers the question. Use the stamp to create a picture that explains your answer." One student's response is shown in Figure 2.
Figure 2: A student's response for a division problem.

The solution shown above suggests that the student had mastered the material because she reached a correct answer for both a number sentence and a pictorial representation of the problem. The teacher had no way to know from this response, however, whether the student knew the mathematical relationship being described and drew the picture as an explanation, or used the picture to help figure out the math. The interaction history gave the teacher insight into the student's thinking process: The playback of the interaction history shows the student creating the seed stamp, then placing seeds in 4 rows of 5. She then placed one more seed at the end of each row to create 4 rows of 6, and filled in the number sentence "4 x 6 = 24". This interaction indicated to the teacher that the student did not know how to approach the problem, but that the student instead used information given in the problem to create 4 rows and experiment until she had the required number of seeds. Replaying the interaction histories for other students enabled the teacher to identify those students who completed the number sentence before creating their pictures, which suggested mastery of the material.
We will continue our investigations of the ink replay feature this next year.
Audio explanations. Students were given the opportunity to add audio explanations to their work for several days during the trial. Preliminary observations about use of the audio recording feature are the following. When presented with a choice of explaining their reasoning, the class was generally evenly split between students who provided only a picture, those who provided a picture and an audio explanation, and those who provided a picture and a written explanation. One student out of 16 provided only an oral explanation for one of the problems. For the most part, the oral explanations that accompanied written explanations simply repeated the same words as were written. Both the written and the oral explanations also often restated a number sentence rather than actually explaining the reasoning behind the sentence. Thus it became clear that the students needed a lesson in what makes for a good explanation, regardless of whether that explanation was written or oral. The use of the oral explanations in the classroom, however, was quite interesting. After the students worked through their problems and submitted their responses to the teacher, the teacher chose student work to display for class discussion. She asked students prior to playing their recordings if they were comfortable with her doing so. Interestingly, while some students wanted the teacher to play their recordings, other students who were typically comfortable speaking to the class preferred that their recordings not be played. The teacher speculated about the students' reluctance, saying, "Recording voice may feel less safe to them because they can't take it back. You can scribble out writing." In addition, we suggest that one can modulate an oral response based on feedback, both oral and visual, from listeners. The teacher also speculated that in a classroom culture that supports students in being comfortable about making mistakes and in respectfully disagreeing with their classmates, students might be amenable to sharing recorded explanations.
A couple of logistical observations that we noted: The directional microphones on the tablet computers worked well for recording; background noise was negligible. The tablets' speakers were adequate for students playing back their explanations at their desks, but not for playback to the entire class. The teacher's machine needed external speakers in order for the explanations submitted to her to be heard by the entire class.
We will continue our investigations of the audio recording feature this next year.