Fall 2011 to Spring 2012
Fall 2012 to Spring 2013
Fall 2013 to Spring 2014
Fall 2014 to Spring 2015
Cambridge, Maria L. Baldwin School, Grade 4
Instructional materials:
Investigations In Number, Data and Space, Grade 4, Unit 8
How Many Packages? How Many Groups?
Sessions 1.1—1.4
Math instruction in this teacher's class dealt with 2-digit by 2-digit multiplication problems, focusing in particular on ways of decomposing the problem into several simpler ones. An array model for multiplication is a centerpiece of the strategy toward which students work. Students also practice estimating products by using landmark numbers (e.g. , multiples of 5, multiples of 10) and, throughout the unit, they make up story problems to correspond to the calculations they are doing, to reinforce their understanding of the meaning of multiplication.
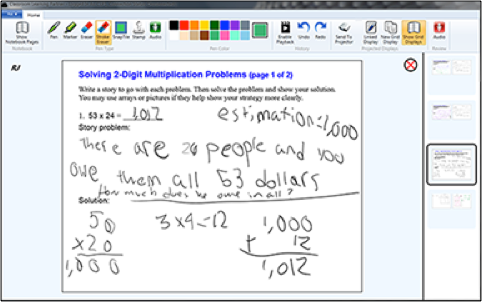
Figure 1 shows a student's work including a story problem to go with the numerical problem, an estimate of the answer to the problem and an exact answer calculated by decomposing the problem into two easier sub-problems.
Figure 1: Student response to 2-digit multiplication problem, including story problem.

As students were submitting their answers to these problems, however, the teacher noticed several answers such as that in Figure 2, in which students had incorrectly decomposed the problem This error is a common one, which the array visualization is specifically meant to address; the teacher was able to realize quickly that a substantial portion of her class was struggling with the decomposition because she had immediate access to the student work on her tablet.
Figure 2: Teacher view of student work showing common error in 2-digit multiplication problem.
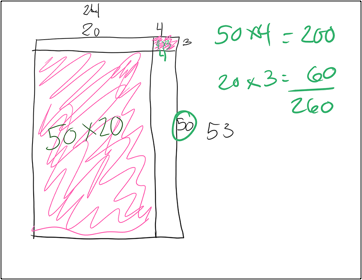
The teacher stopped the class and led a discussion in which she explicitly addressed students' errors, drawing on her tablet the picture in Figure 3. The drawing was projected so that the entire class could see it and also appeared simultaneously in each student's individual notebook. The teacher pointed out that many students, such as the one whose work is shown in Figure 2, were including only the shaded areas in their calculations and were thus leaving out the products in the unshaded portions, represented by the equations in the upper right corner of the page.
Figure 3: Teacher's illustration of array model for 2-digit multiplication.
This explanation and picture helped many of the students, and the next day, a significant portion of the student work reflected the array structure, as shown in Figure 4.
Figure 4: Student work using array model for 2-digit multiplication.

For some students, however, the array structure still seemed too abstract, as it does not distinguish between the size of the group and the number of groups. The Investigations curriculum provides a Teaching Note that offers another option that reflects the structure of a multiplicative situation more clearly, using sketches rather than arrays. The teacher discovered this Note and decided to share the approach with the class, using her tablet to draw and project the picture in Figure 5. The picture represents the situation: 42 bags of 38 apples. The bags of 38 apples are represented as bags of 30 with 8 more added.
Figure 5: Sketch representation of 38 x 42, drawn by the teacher.
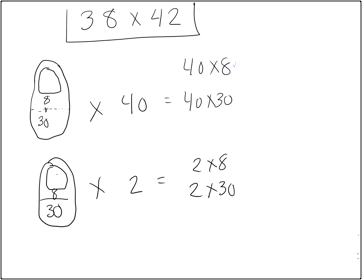
Our work in this teacher's class provided evidence of the usefulness of several aspects of the INK-12 technology. Because she was able to review student work easily during class on her tablet, the teacher was able to detect a problem common to several students and intervene promptly. She did so using her tablet as an "overhead projector," so that what she drew was immediately projected for the entire class to see. Because of the wireless network linking the tablets, however, her drawing also appeared—and was saved—on each student's notebook. Thus, when she went around to help individual students who were still having trouble later, she was able to refer to her explanatory drawing in the students' notebooks.